Cho hình lập phương ABCD.A'B'C'D' góc giữa đường thẳng A'C' và mặt phẳng ( BCC'B' ) bằng:

Câu hỏi
Nhận biếtCho hình lập phương \(ABCD.A'B'C'D'\), góc giữa đường thẳng \(A'C'\) và mặt phẳng \(\left( {BCC'B'} \right)\) bằng:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
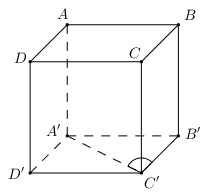
Ta có \(\left\{ \begin{array}{l}A'B' \bot BB'\\A'B' \bot B'C'\end{array} \right. \Rightarrow A'B' \bot \left( {BCC'B'} \right)\)
\( \Rightarrow B'C'\) là hình chiếu của \(A'C'\) lên \(\left( {BCC'B'} \right)\).
\( \Rightarrow \angle \left( {A'C';\left( {BCC'B'} \right)} \right) = \angle \left( {A'C';B'C'} \right) = \angle A'C'B' = {45^0}\).
Vậy \(d\left( {A'C';\left( {BCC'B'} \right)} \right) = {45^0}\).
Chọn A.









