Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính khoảng từ điểm B đến mặt phẳng ( AB'C ).

Câu hỏi
Nhận biếtCho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Tính khoảng từ điểm B đến mặt phẳng \(\left( {AB'C} \right)\).
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
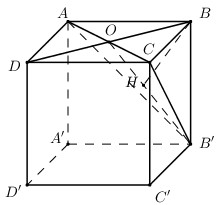
Gọi \(O = AC \cap BD\) ta có: \(\left\{ \begin{array}{l}AC \bot BO\\AC \bot BB'\end{array} \right. \Rightarrow AC \bot \left( {OBB'} \right)\).
Trong \(\left( {OBB'} \right)\) kẻ \(BH \bot OB'\,\,\left( {H \in OB'} \right)\) ta có:
\(\left\{ \begin{array}{l}BH \bot OB'\\BH \bot AC\,\,\left( {AC \bot \left( {OBB'} \right)} \right)\end{array} \right. \Rightarrow BH \bot \left( {AB'C} \right)\)
\( \Rightarrow d\left( {B;\left( {AB'C} \right)} \right) = BH\).
\(ABCD\) là hình vuông cạnh \(a \Rightarrow OB = \dfrac{{a\sqrt 2 }}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông \(OBB'\) ta có: \(BH = \dfrac{{OB.BB'}}{{\sqrt {O{B^2} + BB{'^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a}}{{\sqrt {\dfrac{{{a^2}}}{2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{3}\).
Vậy \(d\left( {B;\left( {AB'C} \right)} \right) = \dfrac{{a\sqrt 3 }}{3}\).
Chọn C.









