Cho hình hộp ABCD.A'B'C'D'. Gọi M,N lần lượt là trung điểm AD,C'D'. C

Câu hỏi
Nhận biếtCho hình hộp \(ABCD.A'B'C'D'\). Gọi \(M,\,\,N\) lần lượt là trung điểm \(AD,\,\,C'D'\). Chứng minh rằng ba vectơ \(\overrightarrow {MN} ,\,\,\overrightarrow {AC'} ,\,\,\overrightarrow {DD'} \) đồng phẳng.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
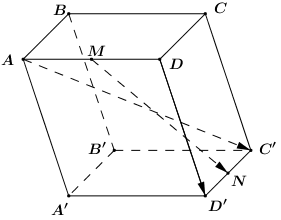
Vì \(N\) là trung điểm của \(C'D'\) nên ta có:
\(\begin{array}{l}\overrightarrow {MN} = \dfrac{1}{2}\left( {\overrightarrow {MC'} + \overrightarrow {MD'} } \right)\\\overrightarrow {MN} = \dfrac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {AC'} + \overrightarrow {MD} + \overrightarrow {DD'} } \right)\\\overrightarrow {MN} = \dfrac{1}{2}\left( { - \dfrac{1}{2}\overrightarrow {AD} + \overrightarrow {AC'} + \dfrac{1}{2}\overrightarrow {AD} + \overrightarrow {DD'} } \right)\\\overrightarrow {MN} = \dfrac{1}{2}\left( {\overrightarrow {AC'} + \overrightarrow {DD'} } \right)\end{array}\)
Vậy ba vectơ \(\overrightarrow {MN} ,\,\,\overrightarrow {AC'} ,\,\,\overrightarrow {DD'} \) đồng phẳng.









