Cho hình hộp ABCD.A'B'C'D'. Gọi G và G' là trọng tâm các tam giác BDA' và A’CC’. Khẳng định nào sau

Câu hỏi
Nhận biếtCho hình hộp ABCD.A'B'C'D'. Gọi G và G' là trọng tâm các tam giác BDA' và A’CC’. Khẳng định nào sau đây đúng?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
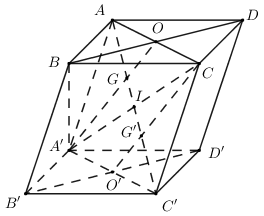
Gọi \(O = AC \cap BD,\,\,O' = A'C' \cap B'D',I = AC' \cap A'C\).
Do ACC’A’ là hình bình hành => I là trung điểm của A’C \(\Rightarrow G \in AI \Rightarrow G \in AC'\). Chứng minh tương tự ta có \(G' \in AC'\).
Do G là trọng tâm tam giác BDA’ nên \(\frac{{A'G}}{{OG}} = 2\).
Áp dụng định lí Ta-lét ta có: \(\frac{{A'G}}{{OG}} = \frac{{GC'}}{{AG}} = 2 \Rightarrow AG = \frac{1}{3}AC'\).
Chứng minh tương tự ta có \(G'C' = \frac{1}{3}AC'\). Vậy \(GG' = \frac{1}{3}AC'\).
Chọn D.









