Cho hình chóp SABCD có đáy ABCD là một tứ giác (AB không song song với CD). Gọi M là trung điểm của
Câu hỏi
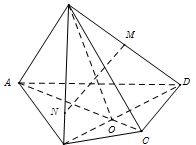
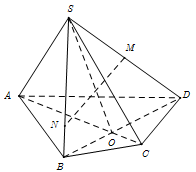
Nhận biếtCho hình chóp S,ABCD có đáy ABCD là một tứ giác (AB không song song với CD). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB sao cho \(SN=2NB\), O là giao điểm của AC và BD. Cặp đường thẳng nào sau đây cắt nhau:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Ta thấy các cặp đường thẳng ở đáp án A, B, C đều chéo nhau nên không thể cắt nhau.
MN và SO cùng thuộc mặt phẳng (SBD). Mà \(\frac{SM}{SD}\ne \frac{SN}{SB}\,\,\left( \frac{1}{2}\ne \frac{2}{3} \right)\Rightarrow \) MN và SO không song song. Chứng tỏ chúng cắt nhau.
Chọn D.










