Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D có AD = CD = a AB = 2a. Cạnh SA vuô

Câu hỏi
Nhận biếtCho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D, có AD = CD = a, AB = 2a. Cạnh SA vuông góc với đáy (ABCD), E là trung điểm của AB. Mệnh đề nào dưới đây sai ?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
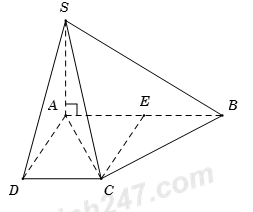
Từ giả thết suy ra ADCE là hình vuông \( \Rightarrow \left\{ \begin{array}{l}CE \bot AB\\CE = AD = a\end{array} \right..\)
Ta có \(\left\{ \begin{array}{l}CE \bot AB\\CE \bot SA{\rm{ }}\left( {{\rm{do }}SA \bot ABCD} \right)\end{array} \right. \Rightarrow CE \bot \left( {SAB} \right).\) Do đó A đúng.
Vì \(CE = AD = a \Rightarrow CE = \frac{1}{2}AB \Rightarrow \Delta ABC\) vuông tại \(C \Rightarrow CB \bot AC\). Kết hợp với \(CB \bot SA\) (do \(SA \bot \left( {ABCD} \right)\)) nên suy ra \(CB \bot \left( {SAC} \right).\) Do đó B đúng.
Ta có
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA{\rm{ }}\left( {{\rm{do }}SA \bot ABCD} \right)\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD \Rightarrow \Delta SCD\) vuông tại D. Do đó C đúng.
Dùng phương pháp loại trừ, suy ra D là đáp án sai.
Chọn D.









