Cho hình chóp S.ABCD với đáy ABCD là hình bình hành tâm O. Cho AD = a tam giác SAD là tam giác đều.

Câu hỏi
Nhận biếtCho hình chóp S.ABCD với đáy ABCD là hình bình hành tâm O. Cho AD = a, tam giác SAD là tam giác đều. Gọi I là trọng tâm tam giác BCD. Mặt phẳng \(\left( \alpha \right)\) đi qua I song song với SA và BC. Thiết diện tạo bởi hình chóp S.ABCD và \(\left( \alpha \right)\)có chu vi là:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
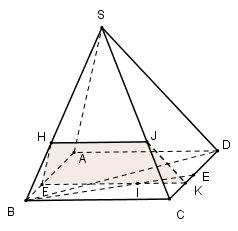
Trong (ABCD) qua I kẻ đường thẳng song song với BC cắt AB và CD lần lượt tại F và K.
Suy ra \(\left( \alpha \right)\cap \left( ABCD \right)=FK\)
Trong (SAB) qua F kẻ FH // SA \(\left( H\in SA \right)\Rightarrow \left( \alpha \right)\cap \left( SAB \right)=FH\)
Trong (SBC) qua H kẻ HJ // BC \(\left( J\in SC \right)\Rightarrow \left( \alpha \right)\cap \left( SBC \right)=HJ\)
Vậy thiết diện của hình chóp khi cắt bởi mp\(\left( \alpha \right)\( là tứ giác KFHJ.
Có HJ // FK nên KFHJ là hình thang.
Ta có: IK // BC nên áp dụng định lí Ta-let: \(\frac{IK}{BC}=\frac{IE}{BE}=\frac{EK}{EC}=\frac{1}{3}\( (với E là trung điểm của CD)
\(\Rightarrow \frac{CK}{CE}=\frac{2}{3}\Rightarrow\frac{CK}{CD}=\frac{1}{3}=\frac{BE}{AB}=\frac{HE}{SA}\Rightarrow HE=\frac{a}{3}\)
HJ // BC \(\Rightarrow \frac{HJ}{BC}=\frac{SH}{SB}=\frac{AE}{AB}=\frac{2}{3}\Rightarrow HJ=\frac{2}{3}BC=\frac{2}{3}a\)
\(\begin{array}{l}\frac{{HJ}}{{BC}} = \frac{{SJ}}{{SC}} = \frac{2}{3} \Rightarrow \frac{{CJ}}{{CS}} = \frac{1}{3}\\ \Rightarrow \frac{{CJ}}{{CS}} = \frac{{CK}}{{CD}} = \frac{1}{3} \Rightarrow IK\parallel SD,\frac{{JK}}{{SD}} = \frac{{CJ}}{{CS}} = \frac{1}{3} \Rightarrow IK = \frac{a}{3}\end{array}\)
Suy ra KFHJ là hình thang cân.
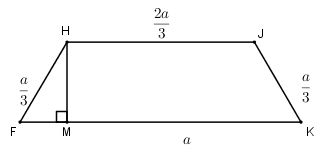
Chu vi hình thang KFHJ là: \[\frac{a}{3}+\frac{a}{3}+\frac{2a}{3}+a=\frac{7a}{3}\]
Chọn A.









