Cho hình chóp S.ABCD. Gọi O=ACcap BD. Một mặt phẳng ( alpha ) cắt SA SB SC SD tại A’ B’ C’ D’. Giả

Câu hỏi
Nhận biếtCho hình chóp S.ABCD. Gọi \(O=AC\cap BD.\) Một mặt phẳng \(\left( \alpha \right)\) cắt SA, SB, SC, SD tại A’, B’, C’, D’. Giả sử \(AB\cap CD=E,A'B'\cap C'D'=E'.\) Tìm phát biểu đúng trong các phát biểu sau:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
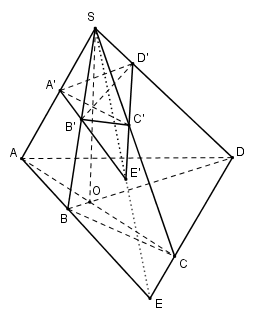
Trong (ABCD) có: \(AB \cap CD = E \Rightarrow \left( {SAB} \right) \cap \left( {SCD} \right) = SE.\)
Ta có: \(\left\{ \begin{array}{l}\left( {A'B'C'D'} \right) \cap \left( {SAB} \right) = A'B'\\\left( {A'B'C'D'} \right) \cap \left( {SCD} \right) = C'D'\\\left( {SAB} \right) \cap \left( {SCD} \right) = SE\end{array} \right. \Rightarrow \) A’B’, C’D’, SE dồng quy. Mà hay 3 điểm S, E. E’ thẳng hàng.
Chọn A.









