Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và SA bot ( A

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD \), đáy \(ABCD \) là hình vuông cạnh bằng \(a \) và \(SA \bot \left( {ABCD} \right). \) Biết \(SA = \dfrac{{a \sqrt 6 }}{3} \). Tính góc giữa \(SC \) và \( \left( {ABCD} \right). \)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
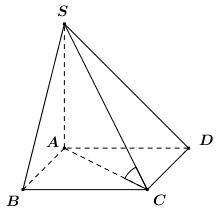
Vì \(SA \bot \left( {ABCD} \right)\) nên \(AC\) là hình chiếu của \(SC\) lên \(\left( {ABCD} \right)\).
\( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA\).
Do \(ABCD\) là hình vuông cạnh \(a\) nên \(AC = a\sqrt 2 \).
Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC\) \( \Rightarrow \Delta SAC\) vuông tại \(A\).
Xét tam giác vuông \(SAC\) ta có: \(\tan \angle SCA = \dfrac{{SA}}{{AC}} = \dfrac{{\dfrac{{a\sqrt 6 }}{3}}}{{a\sqrt 2 }} = \dfrac{{\sqrt 3 }}{3}\).
Vậy \(\angle SCA = {30^0}\) hay \(\angle \left( {SC;\left( {ABCD} \right)} \right) = {30^0}\).
Chọn C.









