Cho hình chóp S.ABCD có O là giao điểm của AC và BD. Giao tuyến của hai mặt phẳng ( SAO ) và ( SBD )

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có \(O\) là giao điểm của \(AC\) và \(BD\). Giao tuyến của hai mặt phẳng \(\left( {SAO} \right)\) và \(\left( {SBD} \right)\) là đường thẳng:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
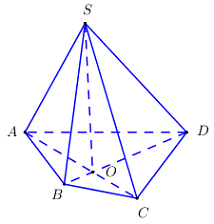
Dễ thấy \(\left( {SAO} \right)\) và \(\) có 1 điểm chung là \(S\).
Ta có \(O = AC \cap BD \Rightarrow \left\{ \begin{array}{l}O \in AO \subset \left( {SAO} \right)\\O \in BD \subset \left( {SBD} \right)\end{array} \right. \Rightarrow O \in \left( {SAO} \right) \cap \left( {SBD} \right)\).
Vậy \(\left( {SAO} \right) \cap \left( {SBD} \right) = SO\) với \(O = AC \cap BD\).
Chọn D.









