Cho hình chóp S.ABCD có đáy là hình vuông cạnh a cạnh bên SA = a và vuông góc với mặt đáy ( ABCD ).

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên \(SA = a\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Tính số đo góc giữa hai đường thẳng SB và CD.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
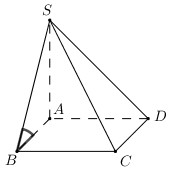
Ta có \(AB//SC \Rightarrow \angle \left( {SB;CD} \right) = \angle \left( {SB;AB} \right) = \angle SBA\)
Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB \Rightarrow \Delta SAB\) vuông tại \(A\).
Lại có \(SA = AB = a \Rightarrow \Delta SAB\) vuông cân tại \(A\).
\( \Rightarrow \angle SBA = {45^0} \Rightarrow \angle \left( {SB;CD} \right) = {45^0}\).
Chọn B.









