Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lầ

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh bằng \(a\) và các cạnh bên đều bằng \(a\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AD\) và \(SD\). Số đo của góc \(\left( {MN;SC} \right)\) bằng:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
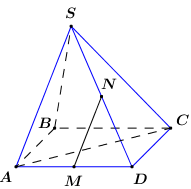
Vì \(ABCD\) là hình chữ nhật cạnh \(a\) nên \(AC = a\sqrt 2 \).
Xét tam giác \(SAC\) ta có: \(A{C^2} = 2{a^2} = S{A^2} + S{C^2}\).
\( \Rightarrow \Delta SAC\) vuông tại \(S\) (Định lí Pytago đảo).
Vì \(MN\) là đường trung bình của tam giác \(SAD\) nên \(MN = \dfrac{1}{2}SA\)
\( \Rightarrow \overrightarrow {NM} = \dfrac{1}{2}\overrightarrow {SA} \).
Khi đó ta có: \(\overrightarrow {NM} .\overrightarrow {SC} = \dfrac{1}{2}\overrightarrow {SA} .\overrightarrow {SC} = 0\).
Vậy \(\left( {MN;SC} \right) = {90^0}\).
Chọn C.









