Cho hình chóp S.ABCD có đáy là hình thang ABCD với AD//BC và AD = 2BC. Gọi M là điểm trên cạnh SD th

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy là hình thang ABCD với \(AD//BC\) và \(AD = 2BC\). Gọi M là điểm trên cạnh SD thỏa mãn \(SM=\frac{1}{3}SD\). Mặt phẳng \(\left( {ABM} \right)\) cắt cạnh bên SC tại điểm N. Tính tỉ số \(\frac{{SN}}{{SC}}\).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
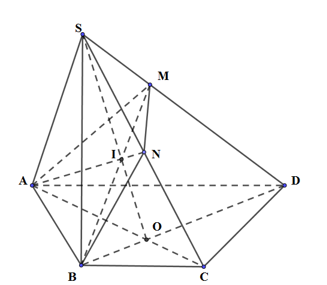
Gọi O là giao điểm của AC và BD; I là giao điểm của SO và BM; N là giao điểm của AI và SC \( \Rightarrow I = \left( {ABM} \right) \cap SC\)
Do ABCD là hình thang với \(AD//BC\) và \(AD = 2BC\), gọi O là giao điểm của AC và BD
\( \Rightarrow \frac{{OC}}{{OA}} = \frac{{OB}}{{OD}} = \frac{{BC}}{{AD}} = \frac{1}{2} \Rightarrow \frac{{OA}}{{AC}} = \frac{{OD}}{{BD}} = \frac{2}{3}\)
\( \Rightarrow OM//SB\) và \(\frac{{OM}}{{SB}} = \frac{2}{3}\) \( \Rightarrow \frac{{IO}}{{IS}} = \frac{{MO}}{{SB}} = \frac{2}{3}\)
Kẻ \(OJ//AN,\,\left( {J \in AN} \right)\)
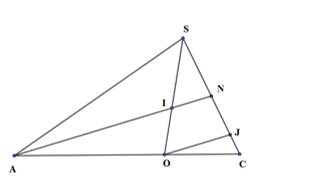
Xét tam giác ANC có: \(OJ//AN,\,\,\frac{{OA}}{{AC}} = \frac{2}{3} \Rightarrow \frac{{NJ}}{{NC}} = \frac{2}{3}\,\, \Rightarrow \overrightarrow {NJ} = \frac{2}{3}\overrightarrow {NC} \)
Xét tam giác ANC có: \(IN//OJ,\,\,\frac{{SI}}{{IO}} = \frac{3}{2} \Rightarrow \frac{{SN}}{{NJ}} = \frac{3}{2}\,\, \Rightarrow \overrightarrow {SN} = \frac{3}{2}\overrightarrow {NJ} \) \( \Rightarrow \overrightarrow {SN} = \overrightarrow {NC} \Rightarrow \overrightarrow {SN} = \frac{1}{2}\overrightarrow {SC} \Rightarrow \frac{{SN}}{{SC}} = \frac{1}{2}\).
Chọn: A









