Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi MNP lần lượt là trung điểm của AB CD SA (Tham khả

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB\), \(CD\), \(SA\) (Tham khảo hình vẽ). Có bao nhiêu khẳng định đúng trong các khẳng định sau
i)\(\left( {MNP} \right)\parallel \left( {SBC} \right).\) ii)\(NP\parallel \left( {SBC} \right).\) 3i)\(MP\parallel \left( {SCD} \right).\) 4i)\(MP\parallel \left( {SBC} \right).\)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
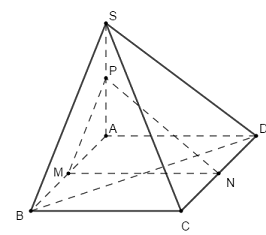
Ta có \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB,\,\,CD,\,\,SA\).
Nên ta có \(\left\{ \begin{array}{l}MN\parallel BC\\MP\parallel SB\end{array} \right. \Rightarrow \left( {MNP} \right)\parallel \left( {SBC} \right) \Rightarrow \left\{ \begin{array}{l}NP\parallel \left( {SBC} \right)\\MP\parallel \left( {SBC} \right)\end{array} \right.\)
Ta có \(MP\parallel SB\); SB cắt \(\left( {SCD} \right)\) tại S nên MP không song song với \(\left( {SCD} \right)\).
Vậy mệnh đề đúng là I;II;IV
Chọn C.









