Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi, O là giao điểm của ha

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Thiết diện của hình chóp khi cắt bởi mặt phẳng \( \left( \alpha \right) \) qua O song song với AB và SC là hình gì?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
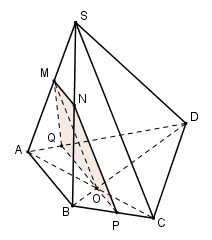
Trong (ABCD) qua O kẻ PQ // AB \(\left( P\in BC,Q\in AD \right)\Rightarrow \left( \alpha \right)\cap \left( ABCD \right)=PQ\)
Trong (SAC) qua O kẻ OM // SC \(\left( M\in SA \right)\Rightarrow \left( \alpha \right)\cap \left( SAD \right)=MQ.\)
Trong (SAB) qua M kẻ MN // AB \(\left( N\in SB \right)\Rightarrow \left( \alpha \right)\cap \left( SAB \right)=MN\)
\(\Rightarrow \left( \alpha \right)\cap \left( SBC \right)=NP\) và NP // AC.
Vậy thiết diện tạo bởi mp\(\left( \alpha \right)\) và hình chóp là tứ giác MNPQ.
Ta có MN // PQ // AB nên MNPQ là hình thang.
Ta có MN // OM. Mà \(OM\cap MQ=M\Rightarrow \) NP và MQ không song song với nhau.
Vậy MNPQ là hình thang.
Chọn D.









