Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng 4a. Cạnh bên SA = 2a. Hình chiếu vuôn

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 4a. Cạnh bên SA = 2a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm của H của đoạn thẳng AO. Gọi \(\alpha \) là góc giữa SD và mặt phẳng (ABCD). Mệnh đề nào sau đây đúng?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
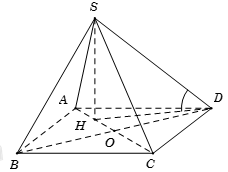
Vì \(SH \bot \left( {ABCD} \right)\) nên hình chiếu vuông góc của SD trên mặt phẳng (ABCD) là HD.
Do đó \(\widehat {\left( {SD,\left( {ABCD} \right)} \right)} = \widehat {\left( {SD,HD} \right)} = \widehat {SDH}.\)
● Tính được
\(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {S{A^2} - {{\left( {\frac{{AC}}{4}} \right)}^2}} = \sqrt {4{a^2} - {{\left( {\frac{{4a\sqrt 2 }}{4}} \right)}^2}} = a\sqrt 2 .\)
● Trong tam giác ADH, có
\(DH = \sqrt {A{H^2} + A{D^2} - 2AH.AD.\cos {{45}^0}} = \sqrt {{{\left( {\frac{{4\sqrt 2 }}{4}} \right)}^2} + 16{a^2} - 2\frac{{4\sqrt 2 }}{4}.4a.\frac{1}{{\sqrt 2 }}} = a\sqrt {10} .\)Tam giác vuông \(SHD\), có \(\tan \widehat {SDH} = \frac{{SH}}{{HD}} = \frac{{a\sqrt 2 }}{{a\sqrt {10} }} = \frac{{\sqrt 5 }}{5}.\)
Chọn C.









