Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh SA = a căn 3 và vuông góc với mặt phẳn

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh \(SA = a\sqrt 3 \) và vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng SD và mặt phẳng đáy bằng ?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
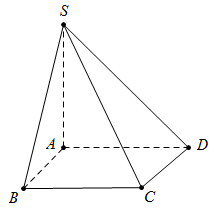
Giao điểm của SD và (ABCD) là D.
Bài ra có \(SA \bot \left( {ABCD} \right)\) tại \(A \Rightarrow \widehat {\left( {SD;\left( {ABCD} \right)} \right)} = \widehat {SDA}.\)
\( \Rightarrow \cos \widehat {\left( {SD;\left( {ABCD} \right)} \right)} = \cos \widehat {SDA} = \frac{{AD}}{{SD}}.\)
Cạnh AD đã biết bằng a, ta cần tính cạnh SD.
Tam giác SAD vuông tại A.
\( \Rightarrow S{D^2} = S{A^2} + A{D^2} = 3{a^2} + {a^2} \Rightarrow SD = 2a\)
\( \Rightarrow \cos \widehat {\left( {SD;\left( {ABCD} \right)} \right)} = \frac{a}{{2a}} = \frac{1}{2}.\)
Chọn B.









