Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn là AB. Điểm M là trung điểm CD. Mặt phẳng ( a

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là AB. Điểm M là trung điểm CD. Mặt phẳng \(\left( \alpha \right)\) qua M, song song với BC và SA. Mặt phẳng\(\left( \alpha \right)\) cắt AB tại E và cắt SB tại F. Thiết diện của hình chóp \(S.ABCD\) cắt bởi \(\left( \alpha \right)\) là hình gì?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
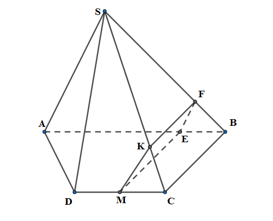
Trong \(\left( {ABCD} \right)\) kẻ \(ME//CD,\,\left( {E \in AB} \right)\)
Trong \(\left( {SAB} \right)\) kẻ \(EF//SA,\,\left( {F \in SB} \right)\)
Trong \(\left( {SBC} \right)\) kẻ \(FK//BC,\,\left( {K \in SC} \right)\)
Khi đó, \(\left( {MEFK} \right)\) là mặt phẳng qua M và song song với BC và SA\( \Rightarrow \left( {MEFK} \right) \equiv \left( \alpha \right)\)
Thiết diện của hình chóp \(S.ABCD\) cắt bởi \(\left( \alpha \right)\) là tứ giác MEFK
Ta có: \(KF//ME\left( {//BC} \right) \Rightarrow MEFK\)là hình thang
Do \(MEBC\) là hình bình hành \( \Rightarrow ME = BC\)
\(KF//BC \Rightarrow \frac{{KF}}{{BC}} = \frac{{SF}}{{SB}} < 1 \Rightarrow KF < BC \Rightarrow KF < ME\)
\( \Rightarrow MEFK\)là hình thang có đáy lớn là ME.
Chọn: C









