Cho hình chóp S.ABCD có đáy ABCD là hình thang có các đáy AD và BC. Gọi M là trọng tâm tam giác SAD
Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình thang có các đáy AD và BC. Gọi M là trọng tâm tam giác SAD, N là điểm thuộc AC sao cho \(NA = {{NC} \over 2}\), P là điểm thuộc đoạn CD sao cho \(PD = {{PC} \over 2}\). Khi đó mệnh đề nào sau đây là đúng?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
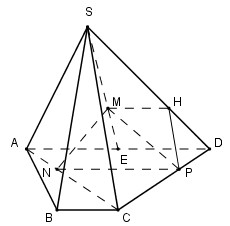
Gọi \(H \in SD\) sao cho \(HD = {1 \over 2}SH\)
Ta có: \({{SM} \over {SE}} = {{SH} \over {SD}} = {2 \over 3} \Rightarrow MH//AD//NP \Rightarrow M,H,P,N\) đồng phẳng.
Ta có:
\(\eqalign{ & {{AN} \over {AC}} = {{DP} \over {DC}} = {1 \over 3} \Rightarrow NP//AD;\,\,{{DH} \over {DS}} = {{DP} \over {DC}} = {1 \over 3} \Rightarrow HP//SC \cr & \left\{ \matrix{ NP//AD//BC \hfill \cr HP//SC \hfill \cr} \right. \Rightarrow \left( {MHPN} \right)//\left( {SBC} \right) \Rightarrow \left( {MNP} \right)//\left( {SBC} \right) \cr & MN \subset \left( {MNP} \right) \Rightarrow MN//\left( {SBC} \right) \cr} \)
Chọn A.
