Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a AD = a căn 3 . Hình chiếu vuông góc H

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, \(AD = a\sqrt 3 \). Hình chiếu vuông góc H của S trên mặt đáy trùng với trọng tâm tam giác ABC và \(SH = \frac{a}{2}\). Gọi M, N lần lượt là trung điểm các cạnh BC và SC. Gọi \(\alpha \) là góc giữa đường thẳng MN với mặt đáy (ABCD). Mệnh đề nào sau đây đúng?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
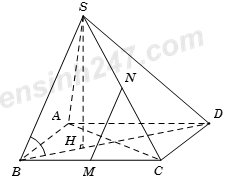
Ta có MN // SB. Do đó \(\widehat {\left( {MN;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;\left( {ABCD} \right)} \right)}\).
Do \(SH \bot \left( {ABCD} \right)\) nên suy ra
\(\widehat {\left( {MN;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;HB} \right)} = \widehat {SBH}\).
Ta có \(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{a^2} + 3{a^2}} = 2a;\,\,BH = \frac{{BD}}{3} = \frac{{2a}}{3}\).
Tam giác SHB, có \(\tan \widehat {SBH} = \frac{{SH}}{{BH}} = \frac{{\frac{a}{2}}}{{\frac{{2a}}{3}}} = \frac{3}{4}\).
Chọn B.









