Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật SA vuông góc với đáy AB = aAD = a căn 3 SA = a. S
Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA\) vuông góc với đáy, \(AB = a,\,\,AD = a\sqrt 3 ,\,\,SA = a\). Số đo góc giữa \(SD\) và mặt phẳng \(\left( {SAB} \right)\) bằng:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
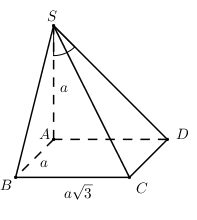
Ta có: \(\left\{ \begin{array}{l}DA \bot AB\\DA \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow DA \bot \left( {SAB} \right)\)
\( \Rightarrow SA\) là hình chiếu của \(SD\) trên \(\left( {SAB} \right)\).
\( \Rightarrow \angle \left( {SD;\left( {SAB} \right)} \right) = \angle \left( {SD;SA} \right) = \angle ASD\)
Xét tam giác vuông \(SAD\) ta có:
\(\tan \angle ASD = \dfrac{{AD}}{{SA}} = \sqrt 3 \Rightarrow \angle ASD = {60^0}\).
Vậy \(\angle \left( {SD;\left( {SAB} \right)} \right) = {60^0}\).
Chọn C.
