Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều. Một mặt phẳng (P) song s

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều. Một mặt phẳng (P) song song với (SBD) và đi qua điểm I thuộc cạnh AC (không trùng với A hoặc C). Thiết diện của (P) với hình chóp là hình gì ?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
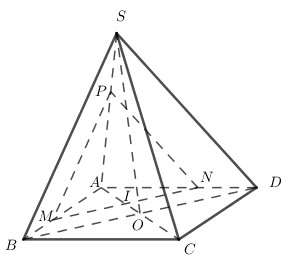
Trong (ABCD) qua I kẻ MN // BD \(\left( {M \in AB;N \in AD} \right)\)
Trong (SAB) qua M kẻ MP // SB \(\left( {P \in SA} \right)\)
\( \Rightarrow \left( {MNP} \right)//\left( {SBD} \right) \Rightarrow \left( P \right) \equiv \left( {MNP} \right)\)
\(\left\{ \matrix{ \left( {MNP} \right) \cap \left( {SAD} \right) = NP \hfill \cr \left( {SBD} \right) \cap \left( {SAD} \right) = SD \hfill \cr \left( {MNP} \right)//\left( {SBD} \right) \hfill \cr} \right. \Rightarrow NP//SD\)
Theo định lí Ta-let ta có: \({{MN} \over {BD}} = {{AM} \over {AB}} = {{AP} \over {AS}} = {{MP} \over {SB}} = {{NP} \over {SD}}\)
Mà tam giác MNP đều.
Chọn D.









