Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O I là trung điểm AO. Thiết diện của hình chó

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm AO. Thiết diện của hình chóp cắt bởi mp(P) qua I và song song với BD, SA là một hình :
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
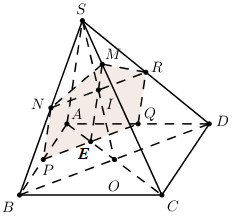
Trong (SAC) qua I kẻ ME // SA \(\left( {M \in SC;E \in AC} \right)\).
Trong (ABCD) qua E kẻ PQ // BD \(\left( {P \in AB;\,\,Q \in AD} \right)\).
Trong (SAB) kẻ PN // SA \(\left( {N \in SB} \right)\), trong (SAD) kẻ QR // SA \(\left( {R \in SD} \right)\).
Vậy thiết diện cần tìm là ngũ giác MNPQR.
Chọn D.









