Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M N K lần lượt là trung điểm của các cạnh DC BC
Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình bình hành. M, N, K lần lượt là trung điểm của các cạnh DC, BC, SA. Gọi H là giao điểm của AC và MN. Giao tuyến của (MNK) với (SAB) là đường thẳng KT, với T được xác định theo 4 phương án liệt kê dưới đây. Hãy chọn câu đúng
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
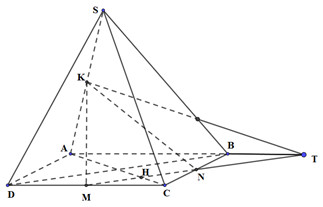
Gọi T là giao điểm của MN với AB. Khi đó:
\(\left\{ \begin{array}{l}T \in MN\\T \in AB \subset \left( {SAB} \right)\end{array} \right. \Rightarrow T = MN \cap \left( {SAB} \right)\).
Chọn: C
