Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi MNPQ lần lượt là trung điểm của các cạnh SAS
Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,\,\,N,\,\,P,\,\,Q\) lần lượt là trung điểm của các cạnh \(SA,\,\,SB,\,\,SC,\,\,SD\). Đường thẳng nào sau đây không song song với đường thẳng \(MN\)?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
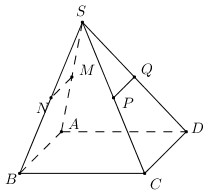
Ta có: \(MN\) là đường trung bình của \(\Delta SAB \Rightarrow MN//AB\).
\(PQ\) là đường trung bình của \(\Delta SCD \Rightarrow PQ//CD\).
Lại có \(ABCD\) là hình bình hành \( \Rightarrow AB//CD\).
Vậy \(MN//AB//CD//PQ\).
Chọn B.
