Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SD điểm N thuộc cạnh SA sao

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SD, điểm N thuộc cạnh SA sao cho SN = 3AN . Đường thẳng MN cắt mặt phẳng (ABCD) tại P, đường thẳng PC cắt cạnh AB tại K . Trình bày cách xác định điểm K và tính tỉ số \(\dfrac{{KA}}{{KB}}\).
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
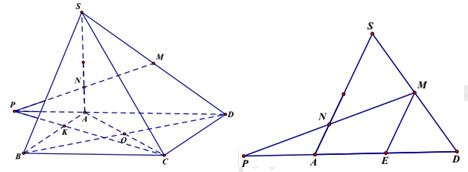
Trong mp(SAD) gọi \(P = MN \cap AD\)
Ta có: \(\left\{ \begin{array}{l}P \in MN\\P \in AD \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow P = MN \cap \left( {ABCD} \right)\)
Trong mp(ABCD) gọi \(K = PC \cap AB\). Khi đó điểm K là điểm cần dựng.
Từ \(SA = 3AN\,\,\left( {gt} \right)\) suy ra \(AN = \dfrac{1}{4}SA\)
Gọi E là trung điểm AD. Ta có ME là đường trung bình của tam giác SAD \( \Rightarrow ME//SA\) \( \Rightarrow AN//ME\).
Áp dụng định lí Talet ta có : \(\dfrac{{PA}}{{PE}} = \dfrac{{AN}}{{ME}} = \dfrac{{\dfrac{1}{4}SA}}{{\dfrac{1}{2}SA}} = \dfrac{1}{2} \Rightarrow \dfrac{{PA}}{{PD}} = \dfrac{1}{3}\)
Trong mặt phẳng (ABCD), có AK / / CD nên ta có: \(\dfrac{{AK}}{{CD}} = \dfrac{{PA}}{{PD}} = \dfrac{1}{3} \Rightarrow \dfrac{{AK}}{{AB}} = \dfrac{1}{3}\,\,\left( {do\,\,AB = CD} \right) \Rightarrow \dfrac{{AK}}{{BK}} = \dfrac{1}{2}\).









