Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAB và I là trung đi

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAB và I là trung điểm của AB. Lấy điểm M trên đoạn AD sao cho \(AD = 3AM\). Đường thẳng qua M và song song với AB cắt CI tại J. Đường thẳng JG không song song với mặt phẳng:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
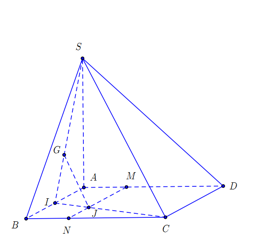
Ta có: \(\frac{{IJ}}{{IC}} = \frac{{AM}}{{AD}} = \frac{1}{3} = \frac{{IG}}{{IS}} \Rightarrow JG//SC \Rightarrow \left\{ \begin{array}{l}JG//\left( {SCD} \right)\\JG//\left( {SAC} \right)\\JG//\left( {SBC} \right)\end{array} \right.\).
Chọn: B









