Cho hình chóp S.ABC có đáyABClà tam giác đều cạnh 2aSAbot ( ABC )SA=a căn 32. Gọi ( P ) là mặt phẳng

Câu hỏi
Nhận biếtCho hình chóp \(S.ABC\) có đáy\(ABC\)là tam giác đều cạnh \(2a,\,\,\,SA\bot \left( ABC \right),\,\,\,SA=\frac{a\sqrt{3}}{2}.\) Gọi \(\left( P \right)\) là mặt phẳng đi qua \(A\) và vuông góc với \(BC.\) Thiết diện của hình chóp \(S.ABC\) được cắt bởi \(\left( P \right)\)có diện tích bằng ?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
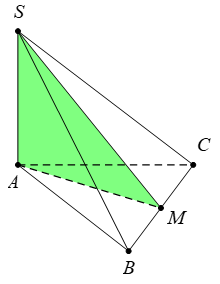
Gọi M là trung điểm của BC thì \(BC\bot AM\,\,\,\,\,\,\,\,\,\left( 1 \right).\)
Hiển nhiên \(AM=\frac{2a\sqrt{3}}{2}=a\sqrt{3}\). Mà \(SA\bot \left( ABC \right)\Rightarrow BC\bot SA\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\,\) và \(\left( 2 \right)\) suy ra \(BC\bot \left( SAM \right)\Rightarrow \left( P \right)\equiv \left( SAM \right).\)
\(\Rightarrow \) Thiết diện của hình chópS.ABC được cắt bởi (P) chính là \(\Delta SAM.\)
Và \(\Delta \,SAM\) vuông tại A nên \({{S}_{\Delta SAM}}=\frac{1}{2}SA.AM=\frac{1}{2}.\frac{a\sqrt{3}}{2}.a\sqrt{3}=\frac{3{{a}^{2}}}{4}.\)
Chọn C.









