Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B cạnh bên SA vuông góc với đáy. Gọi EF lần lượ
Câu hỏi
Nhận biếtCho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,\) cạnh bên \(SA\) vuông góc với đáy. Gọi \(E,\,\,\,F\) lần lượt là trung điểm của cạnh \(AB\) và \(AC.\) Góc giữa hai mặt phẳng \(\left( SEF \right)\) và \(\left( SBC \right)\) là
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
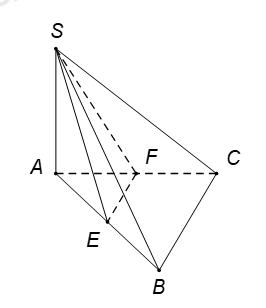
Gọi \(\left( d \right)\) là đường thẳng đi qua \(S\) và song song với EF.
Vì EF là đường trung bình tam giác ABC suy ra EF // BC.
Khi đó d // EF // BC\(\Rightarrow \left( SEF \right)\cap \left( SBC \right)=\left( d \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right).\)
Ta có \(\left\{ \begin{array}{l}SA \bot BC\,\,\,\,\left( {SA \bot \left( {ABC} \right)} \right)\\AB \bot BC\end{array} \right.\)\(\Rightarrow \)
\(BC \bot \left( {SAB} \right) \Rightarrow \left\{ \begin{array}{l}BC \bot SE\\BC \bot SB\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).\)
Từ \(\left( 1 \right),\,\,\left( 2 \right)\) suy ra \(\left\{ \begin{array}{l}\left( d \right) \bot SE\\\left( d \right) \bot SB\end{array} \right. \Rightarrow \widehat {\left( {\left( {SEF} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {SE;SB} \right)} = \widehat {BSE}.\)
Chọn C.
