Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA=SB=SC=b (a>b căn 2). Gọi G là trọng tâmD

Câu hỏi
Nhận biếtCho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và \(SA=SB=SC=b\) (\(a>b\sqrt{2}\)). Gọi \(G\) là trọng tâm\(\Delta \,ABC\). Xét mặt phẳng \(\left( P \right)\) đi qua \(A\) và vuông góc với \(SC\) tại điểm I nằm giữa \(S\) và \(C\). Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( P \right)\) là:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
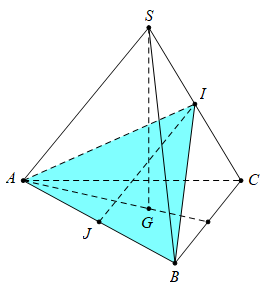
Kẻ \(AI\bot SC\), ta dễ dàng chứng minh được \(\Delta SAI=\Delta SBI\,\,\left( c.g.c \right)\Rightarrow \widehat{SIA}=\widehat{SIB}={{90}^{0}}\Rightarrow BI\bot SC\)
\(\Rightarrow SC\bot \left( ABI \right)\). Thiết diện là tam giác AIB.
Ta có \(AI = AC\sin \widehat {ACS} = a.\sqrt {1 - {{\cos }^2}\widehat {ACS}} = a.\sqrt {1 - {{\left( {\dfrac{{{a^2} + {b^2} - {b^2}}}{{2ab}}} \right)}^2}} = a\sqrt {1 - {{\left( {\frac{a}{{2b}}} \right)}^2}} .\)
Gọi J là trung điểm của AB. Dễ thấy tam giác AIB cân tại I, suy ra \(IJ\bot AB\)
\(\begin{array}{l}
\Rightarrow IJ = \sqrt {A{I^2} - A{J^2}} = \sqrt {{a^2}{{\left( {1 - \dfrac{a}{{2b}}} \right)}^2} - \dfrac{{{a^2}}}{4}} = \sqrt {{a^2}\left( {1 - \dfrac{a}{b} + \dfrac{{{a^2}}}{{4{b^2}}}} \right) - \dfrac{{{a^2}}}{4}} \\
= \sqrt {\dfrac{{{a^2}}}{{4{b^2}}}\left( {4{b^2} - 4ab + {a^2} - {b^2}} \right)} = \dfrac{a}{{2b}}\sqrt {{a^2} + 3{b^2} - 4ab}
\end{array}\)
Do đó: \(S = \dfrac{1}{2}AB.IJ = \dfrac{{{a^2}\sqrt {{a^2} + 3{b^2} - 4ab} }}{{4b}}\)
Chọn A









