Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a SA bot ( ABC ) góc giữa đường thẳng SB và mặt

Câu hỏi
Nhận biếtCho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a,{\rm{ }}SA \bot \left( {ABC} \right),\) góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(60^\circ .\) Gọi \(M\) là trung điểm \(BC\).
a) Chứng minh \(SA \bot AM,\,\,\left( {SAM} \right) \bot \left( {SBC} \right)\).
b) Tính khoảng cách giữa hai đường thẳng \(AC\) và \(SB\).
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
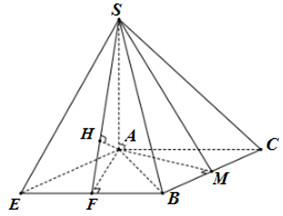
a) Ta có \(\left\{ \begin{array}{l}SA \bot \left( {ABC} \right)\\AM \subset \left( {ABC} \right)\end{array} \right. \Rightarrow SA \bot AM\)
Tam giác ABC đều \( \Rightarrow AM \bot BC\).
Ta có \(\left\{ \begin{array}{l}BC \bot AM\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right)\).
Mà \(BC \subset \left( {SBC} \right) \Rightarrow \left( {SAM} \right) \bot \left( {SBC} \right)\).
b) Dựng hình bình hành ACBE ta có \(AC//BE,\,\,BE \subset \left( {SBE} \right) \Rightarrow AC//\left( {SBE} \right)\)
Lại có \(\left( {SBE} \right) \supset SB \Rightarrow d\left( {AC;SB} \right) = d\left( {AC;\left( {SBE} \right)} \right) = d\left( {A;\left( {SBE} \right)} \right)\).
Gọi F là trung điểm của BE.
Do \(ABC\) là tam giác đều \( \Rightarrow AC = BC = AB \Rightarrow ACBE\) là hình thoi
\( \Rightarrow AC = BC = BE = AE = AB \Rightarrow \Delta ABE\) đều cạnh \(a\) \( \Rightarrow AF \bot BE\).
Trong \(\left( {SAF} \right)\) kẻ \(AH \bot SF\,\,\left( {H \in SF} \right)\) ta có : \(\left\{ \begin{array}{l}BE \bot AF\,\,\left( {cmt} \right)\\BE \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BE \bot \left( {SAF} \right) \Rightarrow BE \bot AH\).
\(\left\{ \begin{array}{l}AH \bot SF\\AH \bot BE\end{array} \right. \Rightarrow AH \bot \left( {SBE} \right) \Rightarrow d\left( {A;\left( {SBE} \right)} \right) = AH \Rightarrow d\left( {AC;SB} \right) = AH\)
Ta có \(SA \bot \left( {ABC} \right) \Rightarrow AB\) là hình chiếu của \(SB\) trên \(\left( {ABC} \right)\).
\( \Rightarrow \angle \left( {SB;\left( {ABC} \right)} \right) = \angle \left( {SB;AB} \right) = \angle SBA = {60^0}\).
Xét tam giác vuông \(SAB\) có \(SA = AB.\tan {60^0} = a\sqrt 3 \).
Tam giác \(ABE\) đều cạnh \(a\,\,\left( {cmt} \right) \Rightarrow AF = \dfrac{{a\sqrt 3 }}{2}\).
\( \Rightarrow AH = \dfrac{{SA.AF}}{{\sqrt {S{A^2} + A{F^2}} }} = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {3{a^2} + \dfrac{{3{a^2}}}{4}} }} = \dfrac{{a\sqrt {15} }}{5}\) (hệ thức lượng trong tam giác vuông).









