Cho hình chóp S.ABC có A’ B’ lần lượt là trung điểm SA SB G là trọng tâm tam giác ABC. C’ là điểm di

Câu hỏi
Nhận biếtCho hình chóp S.ABC có A’, B’ lần lượt là trung điểm SA, SB, G là trọng tâm tam giác ABC. C’ là điểm di động trên cạnh SC. Gọi G’ là giao điểm của SG với (A’B’C’). Khi C’ di động trên SC, biểu thức nào sau đây có giá trị không thay đổi?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
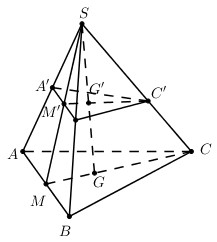
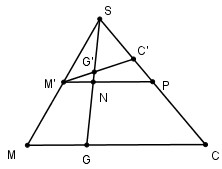
Gọi P là trung điểm của SC, \(N = M'P \cap SG\). Ta dễ dàng chứng minh được N là trung điểm của SG.
Áp dụng định lí Menelaus trong tam giác SNP có : \(\dfrac{{G'S}}{{G'N}}.\dfrac{{M'N}}{{M'P}}.\dfrac{{C'P}}{{C'S}} = 1\,\,\,\left( * \right)\).
Áp dụng định lí Ta-lét ta có : \(\dfrac{{M'N}}{{MG}} = \dfrac{1}{2};\,\,\dfrac{{NP}}{{GC}} = \dfrac{1}{2} \Leftrightarrow \dfrac{{M'N}}{{MG}} = \dfrac{{NP}}{{GC}} \Rightarrow \dfrac{{M'N}}{{NP}} = \dfrac{{MG}}{{GC}} = \dfrac{1}{2} \Rightarrow \dfrac{{M'N}}{{M'P}} = \dfrac{1}{3}\)
Thay vào (*) ta có \(\dfrac{{G'S}}{{G'N}}.\dfrac{1}{3}.\dfrac{{C'P}}{{C'S}} = 1 \Leftrightarrow \dfrac{{G'S}}{{G'N}}.\dfrac{{C'P}}{{C'S}} = 3 \Leftrightarrow \dfrac{{C'P}}{{C'S}} = 3.\dfrac{{G'N}}{{G'S}}\,\,\,\left( {**} \right)\).
Ta có :
\(\begin{array}{l}\dfrac{{G'S}}{{G'N}} = \dfrac{{NG'}}{{SG'}} = \dfrac{{SN - SG'}}{{SG'}} = \dfrac{{\dfrac{1}{2}SG}}{{SG'}} - 1 = \dfrac{1}{2}\dfrac{{SG}}{{SG'}} - 1\\\dfrac{{C'P}}{{C'S}} = \dfrac{{PC'}}{{SC'}} = \dfrac{{SP - SC'}}{{SC'}} = \dfrac{{\dfrac{1}{2}SC}}{{SC'}} - 1 = \dfrac{1}{2}\dfrac{{SC}}{{SC'}} - 1\end{array}\)
Thay vào (**) \( \Rightarrow \dfrac{1}{2}\dfrac{{SC}}{{SC'}} - 1 = 3\left( {\dfrac{1}{2}\dfrac{{SG}}{{SG'}} - 1} \right) \Leftrightarrow \dfrac{1}{2}\left( {3\dfrac{{SG}}{{SG'}} - \dfrac{{SC}}{{SC'}}} \right) = 2 \Leftrightarrow 3\dfrac{{SG}}{{SG'}} - \dfrac{{SC}}{{SC'}} = 4 = const\).
Chọn D.









