Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh a, tâm O; SO=

Câu hỏi
Nhận biếtCho hình chóp đều \(S.ABC \) có đáy \(ABC \) là tam giác đều cạnh \(a \), tâm \(O \); \(SO=2a \). Gọi \(M \) là điểm thuộc đoạn \(AO \text{ } \, \left( M \ne A;M \ne O \right) \). Mặt phẳng \( \left( \alpha \right) \) đi qua \(M \) và vuông góc với \(AO \). Đặt \(AM=x \). Tính diện tích \(S \) của thiết diện tạo bởi \( \left( \alpha \right) \) với hình chóp \(S.ABC. \)
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
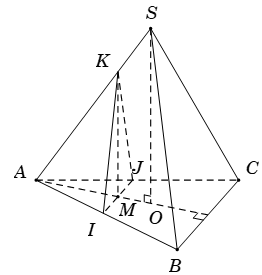
Vì S.ABC là hình chóp đều nên \(SO\bot \left( ABC \right)\) ( với O là tâm của tam giác ABC).
Do đó \(SO\bot AO\) mà \(\left( \alpha \right)\bot AO\) suy ra \(SO\parallel \left( \alpha \right)\).
Tương tự ta cũng có \(BC\parallel \left( \alpha \right)\).
Qua M kẻ \(IJ\parallel BC\) với \(I\in AB,\text{ }J\in AC\); kẻ \(MK\parallel SO\) với \(K\in SA.\)
Khi đó thiết diện là tam giác KIJ.
Diện tích tam giác KIJ là \({{S}_{\Delta IJK}}=\frac{1}{2}IJ.MK\).
Trong tam giác ABC, ta có \(\frac{IJ}{BC}=\frac{AM}{AA'}\) (A’ là trung điểm của BC) suy ra \(IJ=\frac{AM.BC}{AA'}=\frac{x.a}{\frac{a\sqrt{3}}{2}}=\frac{2x\sqrt{3}}{3}\).
Tương tự trong tam giác SAO, ta có \(\frac{MK}{SO}=\frac{AM}{AO}\) suy ra \(MK=\frac{AM.SO}{AO}=\frac{x.2a}{\frac{2}{3}\frac{a\sqrt{3}}{2}}=2x\sqrt{3}\).
Vậy \({{S}_{\Delta IJK}}=\frac{1}{2}\frac{2x\sqrt{3}}{3}.2x\sqrt{3}=2{{x}^{2}}\).
Chọn B









