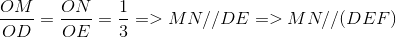Cho hình bình hành ABCD và ABEF không cùng nằm trên 1 mặt phẳng. Trên
Câu hỏi
Nhận biếtCho hình bình hành ABCD và ABEF không cùng nằm trên 1 mặt phẳng. Trên đoạn AC lấy điểm M , trên đoạn BF lấy điểm N thỏa mãn 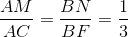. Chứng minh MN // (DEF)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
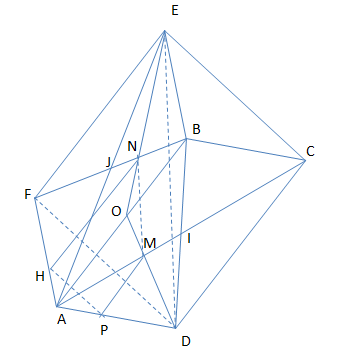
Cách 1 :
Trong (ABCD) vẽ MP // AB
Trong (ABEF) , vẽ NH // AB
=> MP // NH
Do đó 4 điểm M , N , P , H đồng phẳng
Ta có : HN // AB => HN // FE (1)
Do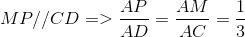 
Do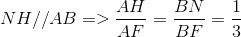 
Vì vậy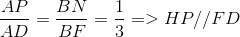 
(2)
Từ (1) và (2) => (MNHP) // (EFDC) => MN // (DEF)
Cách 2 :
Gọi I ; J là tâm các hình bình hành ABCD và ABEF
Từ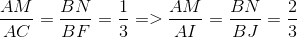 
Do đó M và N lần lượt là trọng tâm tam giác ABD và tam giác ABE nên DM và EN cắt nhau tại trung điểm O của AB
Ta có : 
