Cho hàm số f( x ) = l căn ( x - 3 )^2 x - 3 khix ne 3mx^2 + mx khix = 3 . . Tìm tất cả các giá trị
Câu hỏi
Nhận biếtCho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}}\,\,\,\,\,{\rm{khi}}\,\,x\, \ne 3\\\,\,\,\,\,\,m{x^2} + mx\,\,\,\,{\rm{khi}}\,\,x = 3\end{array} \right.\) . Tìm tất cả các giá trị của tham số thực \(m\) để hàm số liên tục tại \(x = 3\) .
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
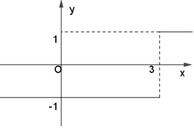
Hàm số đã cho xác định trên \(\mathbb{R}\) .
Ta có :
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{ - \left( {x - 3} \right)}}{{x - 3}} = - 1.\\\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{\left( {x - 3} \right)}}{{x - 3}} = 1.\\\end{array}\)
Vậy \(\mathop {\lim }\limits_{x \to {3^ + }} f(x) \ne \mathop {\lim }\limits_{x \to {3^ - }} f(x)\) nên \(\mathop {\lim }\limits_{x \to 3} f(x)\) không tồn tại.
Vậy với mọi \(m\), hàm số đã cho không liên tục tại \(x = 3.\)
Ta có thể tam khảo thêm đồ thị của hàm số khi để hiểu rõ hơn.
Chọn A.
