Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC=AD=BC=BD=aCD=2x. Với giá

Câu hỏi
Nhận biếtCho hai tam giác \(ACD\) và \(BCD\) nằm trên hai mặt phẳng vuông góc với nhau và \(AC=AD=BC=BD=a,\,\,\,CD=2x.\) Với giá trị nào của \(x\) thì hai mặt phẳng \(\left( ABC \right)\) và \(\left( ABD \right)\) vuông góc.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
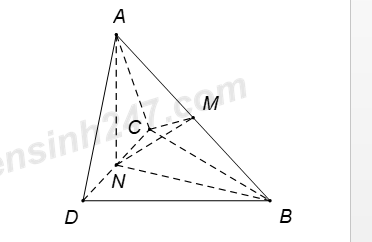
Gọi M, N lần lượt là trung điểm của AB, CD.
Ta có \(AN\bot CD\) mà \(\left( ACD \right)\bot \left( BCD \right)\)
\(\Rightarrow AN\bot \left( BCD \right)\Rightarrow AN\bot BN\Rightarrow \Delta ANB\) vuông tại N \(\Rightarrow NM=\frac{AB}{2}\,\,\left( 1 \right)\)
Tam giác \(ABC\) cân tại \(C,\) có \(M\) là trung điểm của \(AB\)\(\Rightarrow CM\bot AB.\)
Giả sử \(\left( ABC \right)\bot \left( ABD \right)\) mà \(CM\bot AB\)\(\Rightarrow CM\bot \left( ABD \right)\Rightarrow CM\bot DM.\)
Khi đó, \(\Delta \,MCD\) vuông tại \(M\). Ta có \(\Delta ABC=\Delta ABD\,\,\left( c.c.c \right)\Rightarrow CM=DM\Rightarrow \Delta MCD\) vuông cân tại M.
\(\Rightarrow \,\,MN=\frac{CD}{2}\,\,\,\left( 2 \right)\).
Từ (1) và (2) \(\Rightarrow AB=CD=2x\)
Lại có \(\Delta ACD=\Delta BCD\,\,\left( c.c.c \right)\Rightarrow AN=BN=\sqrt{A{{C}^{2}}-C{{N}^{2}}}=\sqrt{{{a}^{2}}-{{x}^{2}}},\) mà \(A{{B}^{2}}=A{{N}^{2}}+B{{N}^{2}}.\)
Suy ra \(2\left( {{a}^{2}}-{{x}^{2}} \right)=4{{x}^{2}}\Leftrightarrow {{a}^{2}}=3{{x}^{2}}\Leftrightarrow x=\frac{a\sqrt{3}}{3}.\)
Chọn A.









