Cho hai đường tròn bằng nhau ( O ) và ( O' ) và tiếp xúc ngoài nhau. C

Câu hỏi
Nhận biếtCho hai đường tròn bằng nhau \( \left( O \right) \) và \( \left( {O'} \right) \) và tiếp xúc ngoài nhau. Có bao nhiêu phép quay góc \({90^0} \) biến đường \( \left( O \right) \) thành \( \left( {O'} \right) \)?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Phép quay tâm \(O\) góc quay \(\alpha \) biến đường tròn thành đường tròn có cùng bán kính.
+ Đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài nhau.
Vẽ \(\Delta AOO'\) vuông cân tại \(A\), \(\Delta BOO'\) vuông cân tại \(B\)
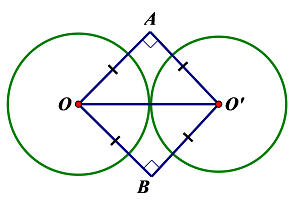
Ta có:
\(\left\{ \begin{array}{l}{Q_{\left( {A;{{90}^0}} \right)}}{\rm{ }}O = O'\\R = R'\end{array} \right.\)\( \Rightarrow \)Phép quay tâm \(A\) biến đường tròn tâm \(O\) thành đường tròn tâm \(O'\) (thỏa mãn ycbt).
+ \(\left\{ \begin{array}{l}{Q_{\left( {B;{{90}^0}} \right)}}O = O'\\R = R'\end{array} \right.\)\( \Rightarrow \)Phép quay tâm \(B\) biến đường tròn tâm \(O\) thành đường tròn tâm \(O'\) (thỏa mãn ycbt).
\( \Rightarrow \) Có 2 phép quay góc \({90^0}\) biến đường tròn tâm \(O\) thành đường tròn tâm \(O'\).
Chọn C.









