Cho đường thẳng Delta và điểm O notin Delta . Một điểm M thay đổi trên Delta . Gọi N là trung điểm

Câu hỏi
Nhận biếtCho đường thẳng \(\Delta \) và điểm \(O \notin \Delta \). Một điểm M thay đổi trên \(\Delta \). Gọi N là trung điểm của đoạn thẳng OM. Khi M thay đổi trên \(\Delta \) tập hợp các điểm N là:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
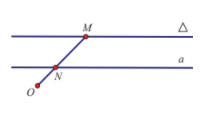
Từ giả thiết ta có \(\overrightarrow {ON} = {1 \over 2}\overrightarrow {OM} \)
\( \Rightarrow \) Phép vị tự tâm O tỉ số \(k = {1 \over 2}\) biến điểm M thành điểm N.
Vậy khi M thay đổi trên \(\Delta \) thì N thay đổi trên đường a là ảnh của \(\Delta \) qua phép vị tự \({V_{\left( {O;{1 \over 2}} \right)}}\).
\( \Rightarrow a//\Delta \) và dễ thấy \(d\left( {O;a} \right) = {1 \over 2}d\left( {O;\Delta } \right)\)
Chọn B.









