Cho chóp đều S.ABCD có cạnh đáy bằng 2 cạnh bên bằng 3. Gọi varphi là góc giữa giữa cạnh bên và mặt

Câu hỏi
Nhận biếtCho chóp đều S.ABCD có cạnh đáy bằng 2, cạnh bên bằng 3. Gọi \(\varphi \) là góc giữa giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
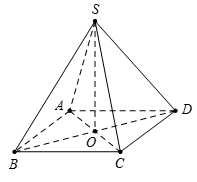
Gọi O là tâm mặt đáy (ABCD), suy ra \(SO \bot \left( {ABCD} \right)\).
Vì \(SO \bot \left( {ABCD} \right)\)\( \Rightarrow \)OA là hình chiếu của SA trên mp(ABCD).
Do đó \(\widehat {\left( {SA;\left( {ABCD} \right)} \right)} = \widehat {\left( {SA;AO} \right)} = \widehat {SAO}.\)
Tam giác vuông SAO, có
\(\tan \widehat {SAO} = \frac{{SO}}{{AO}} = \frac{{\sqrt {S{B^2} - B{O^2}} }}{{AO}} = \frac{{\sqrt {S{B^2} - {{\left( {\frac{{BD}}{2}} \right)}^2}} }}{{\frac{{AC}}{2}}} = \frac{{\sqrt {{3^2} - {{\left( {\frac{{2\sqrt 2 }}{2}} \right)}^2}} }}{{\frac{{2\sqrt 2 }}{2}}} = \frac{{\sqrt {14} }}{2}.\)
Chọn D.









