Cho ΔABC nằm trong mặt phẳng (P) và đường thẳng a nằm trong mặt phẳng

Câu hỏi
Nhận biếtCho \(ΔABC\) nằm trong mặt phẳng \((P)\) và đường thẳng \(a\) nằm trong mặt phẳng \((P)\) không song song với \(AB, AC\). \(S\) là một điểm nằm ngoài mặt phẳng \((P)\) và \(A’\) là một điểm thuộc \(SA\). Xác định giao tuyến của hai mặt phẳng \((A’; a)\) và \((ABC)\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
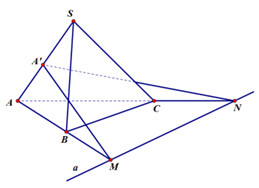
Kẻ đường thẳng AB cắt đường thẳng a tại M. Nối A’M. Khi đó,
· A’M ⊂ (A’; a) và M ∈ (A’; a). · M ∈ AB mà AB ⊂ (ABC) ⇒ M ∈ (ABC)Vậy M là một điểm chung của hai mặt phẳng (A’;a) và (ABC).
Kẻ đường thẳng AC cắt đường thẳng a tại N. Nối A’N. Khi đó,
· A’N ⊂ (A’; a) và N’ ∈ (A’; a). · N ∈ AC mà AC ⊂ (ABC) ⇒ N ∈ (ABC)Vậy N là một điểm chung của hạ mặt phẳng (Á’; a) và (ABC).
Do đó, MN là giao tuyến của hai mặt phẳng (A’; a) và (ABC).









