Các giá trị của m in [ a;b ] để phương trình cos 2x + sin ^2x + 3cos x - m = 5 có nghiệm thì:
![Các giá trị của m in [ a;b ] để phương trình cos 2x + sin ^2x + 3cos x - m = 5 có nghiệm thì:](https://tuhoc365.vn/wp-content/uploads/2020/03/qa-238x145.png "Các giá trị của m in [ a;b ] để phương trình cos 2x + sin ^2x + 3cos x - m = 5 có nghiệm thì:")
Câu hỏi
Nhận biếtCác giá trị của \(m \in \left[ {a;b} \right]\) để phương trình \(\cos 2x + {\sin ^2}x + 3\cos x - m = 5\) có nghiệm thì:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Hướng dẫn giải chi tiết
\(\eqalign{ & \,\,\,\,\,\,\,\,\cos 2x + {\sin ^2}x + 3\cos x - m = 5 \cr & \Leftrightarrow 2{\cos ^2}x - 1 + 1 - {\cos ^2}x + 3\cos x - m - 5 = 0 \cr & \Leftrightarrow {\cos ^2}x + 3\cos x - m - 5 = 0 \cr} \)
Đặt \(t = \cos x\,\,\left( {t \in \left[ { - 1;1} \right]} \right)\) khi đó phương trình trở thành \({t^2} + 3t - 5 = m\)
Xét hàm số \(f\left( t \right) = {t^2} + 3t - 5\) trên \(\left[ { - 1;1} \right]\) ta có BBT:
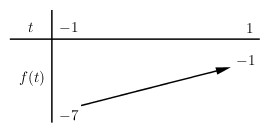
Từ BBT ta thấy: \( - 7 \le f\left( t \right) \le - 1\)
Để phương trình có nghiệm thì \( - 7 \le m \le - 1 \Leftrightarrow m \in \left[ { - 7; - 1} \right]\)
\( \Rightarrow a = - 7,b = - 1 \Rightarrow a + b = - 8\)
Chọn B.
