AI

Câu hỏi
Nhận biết\(\overrightarrow {AI} \)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
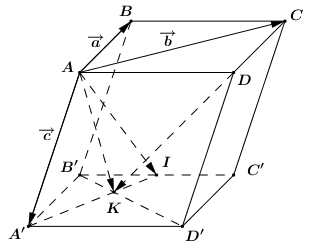
Ta có:
\(\begin{array}{l}\overrightarrow {AI} = \overrightarrow {AA'} + \overrightarrow {A'B'} + \overrightarrow {B'I} \\\,\,\,\,\,\,\, = \overrightarrow c + \overrightarrow a + \dfrac{1}{2}\overrightarrow {B'C'} \\\,\,\,\,\,\,\, = \overrightarrow a + \overrightarrow c + \dfrac{1}{2}\left( {\overrightarrow {A'C'} - \overrightarrow {A'B'} } \right)\\\,\,\,\,\,\,\, = \overrightarrow a + \overrightarrow c + \dfrac{1}{2}\left( {\overrightarrow b - \overrightarrow a } \right)\\\,\,\,\,\,\,\, = \dfrac{1}{2}\overrightarrow a + \dfrac{1}{2}\overrightarrow b + \overrightarrow c \end{array}\)
Chọn C.









