Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M N P theo thứ tự là trung điểm của SA

Câu hỏi
Nhận biếtCho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
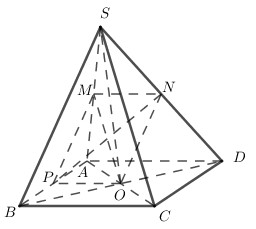
Dễ dàng chứng minh được MNOP là hình bình hành \( \Rightarrow M,N,O,P\) đồng phẳng \( \Rightarrow A,C\) sai.
Ta có : MN là đường trung bình của tam giác SAD \( \Rightarrow MN//AD//BC\)
ON là đường trung bình của tam giác SBD \( \Rightarrow ON//SB\)
\( \Rightarrow \) (MON) // (SBC)
\( \Rightarrow \) Đáp án B đúng.
Đáp án D sai vì \(N \in \left( {MNP} \right) \cap \left( {SBD} \right)\)
Chọn B.









