Trong mặt phẳng ( P ) cho nửa đường tròn đường kính AB=2R và điểm C thuộc nửa đường tròn đó sao cho

Câu hỏi
Nhận biếtTrong mặt phẳng \(\left( P \right)\) cho nửa đường tròn đường kính \(AB=2R\) và điểm \(C\) thuộc nửa đường tròn đó sao cho \(AC=R\). Trên đường thẳng vuông góc với \(\left( P \right)\) tại \(A\) lấy điểm \(S\) sao cho góc giữa hai mặt phẳng \(\left( SAB \right)\) và \(\left( SBC \right)\) bằng \({{60}^{0}}\). Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(A\) lên \(SB,\,\,SC\). Độ dài cạnh \(SA\) tính theo \(R\) là
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
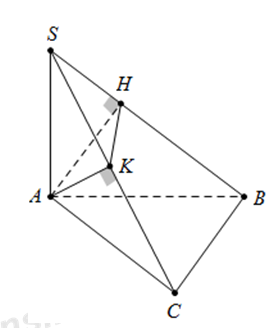
Ta có \(\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot AK\).
Do đó \(AK \bot \left( {SBC} \right) \Rightarrow AK \bot KH\).
\(\begin{array}{l}\left\{ \begin{array}{l}AH \bot SB\\AK \bot SB\end{array} \right. \Rightarrow SB \bot \left( {AHK} \right) \Rightarrow SB \bot HK\\\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\\left( {SAB} \right) \supset AH \bot SB\\\left( {SAC} \right) \supset HK \bot SB\end{array} \right. \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SBC} \right)} \right)} =\widehat {\left( {AH;HK} \right)} = \widehat {AHK} = {60^0}\end{array}\)
Xét tam giác AHK vuông tại K có:
\(AK=AH.\sin {{60}^{0}}\Leftrightarrow A{{K}^{2}}=\frac{3}{4}A{{H}^{2}}\Leftrightarrow \frac{3}{4}\frac{1}{A{{K}^{2}}}=\frac{1}{A{{H}^{2}}}\).
Đặt SA = a, áp dụng hệ thức lượng, ta được
\(\frac{1}{A{{K}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{C}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{R}^{2}}}\) \(\frac{1}{A{{H}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{B}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{4{{R}^{2}}}\)Suy ra \(\frac{3}{4}\left( \frac{1}{{{a}^{2}}}+\frac{1}{{{R}^{2}}} \right)=\frac{1}{{{a}^{2}}}+\frac{1}{4{{R}^{2}}}\Leftrightarrow \frac{1}{4}\frac{1}{{{a}^{2}}}=\frac{1}{2}\frac{1}{{{R}^{2}}}\Leftrightarrow {{a}^{2}}=\frac{{{R}^{2}}}{2}\Leftrightarrow a=\frac{R}{\sqrt{2}}\).
Chọn A.









