Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm SC. Tính góc varphi giữa ha

Câu hỏi
Nhận biếtCho hình chóp đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm \(SC\). Tính góc \(\varphi \) giữa hai mặt phẳng \(\left( MBD \right)\) và \(\left( ABCD \right)\).
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
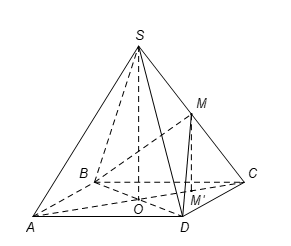
Gọi M’ là trung điểm \(OC\Rightarrow M{M}'\parallel SO\Rightarrow M{M}'\bot \left( ABCD \right).\)
Theo công thức diện tích hình chiếu, ta có \({{S}_{\Delta \,{M}'BD}}=\cos \varphi .{{S}_{\Delta \,MBD}}\)
\(\begin{array}{l} \Rightarrow \cos \varphi = \frac{{{S_{\Delta \,M'BD}}}}{{{S_{\Delta \,MBD}}}} = \frac{{BD.M'O}}{{BD.MO}} = \frac{{M'O}}{{MO}} = \frac{{\frac{1}{2}SO}}{{\frac{1}{2}SA}}\\ = \frac{{\sqrt {S{A^2} - O{A^2}} }}{{SA}} = \frac{{\sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} }}{a} = \frac{{\sqrt 2 }}{2} \Rightarrow \varphi = {45^0}.\end{array}\)
Chọn C.









