Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=a. Tam giác SAB đều và nằm trong mặt phẳng vuô

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB=a.\) Tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng \(SD\) và mặt phẳng \(\left( ABCD \right)\) bằng \({{30}^{0}}.\) Tính diện tích hình chữ nhật \(ABCD.\)
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
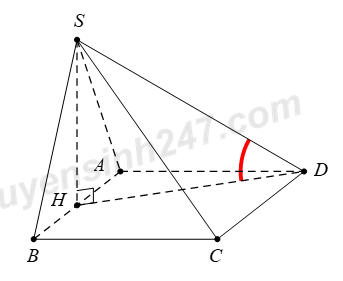
Gọi \(H\) là trung điểm của \(AB,\) tam giác \(SAB\) đều \(\Rightarrow \,\,SH\bot AB.\)
Mà \(\left( SAB \right)\bot \left( ABCD \right)\)\(\Rightarrow \)\(SH\bot \left( ABCD \right)\) và \(SH=\frac{a\sqrt{3}}{2}.\)
Suy ra \(\widehat{SD;\left( ABCD \right)}=\widehat{\left( SD;HD \right)}=\widehat{SDH}={{30}^{0}}.\)
Tam giác \(SHD\) vuông tại \(H,\) có \(\tan \widehat{SDH}=\frac{SH}{HD}\Rightarrow HD=\frac{3a}{2}.\)
Tam giác \(AHD\) vuông tại \(A,\) có \(AD=\sqrt{H{{D}^{2}}-A{{H}^{2}}}=a\sqrt{2}.\)
Vậy diện tích hình chữ nhật \(ABCD\) là \({{S}_{ABCD}}=\sqrt{2}\,{{a}^{2}}.\)
Chọn B









