Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D AB=2atext AD=DC=a; cạnh bên SA=a và

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(AB=2a,\text{ }AD=DC=a\); cạnh bên \(SA=a\) và vuông góc với đáy. Mặt phẳng \(\left( \alpha \right)\) qua \(SD\) và vuông góc với mặt phẳng \(\left( SAC \right)\). Tính diện tích \(S\) của thiết diện tạo bởi \(\left( \alpha \right)\) với hình chóp đã cho.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
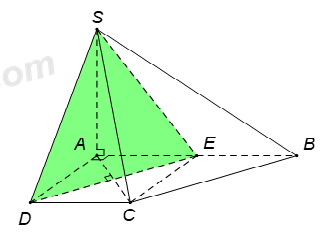
Gọi \(E\) là trung điểm \(AB\).
Suy ra \(AECD\) là hình vuông nên \(DE\bot AC\). \(\left( 1 \right)\)
Mặt khác \(SA\bot \left( ABCD \right)\Rightarrow SA\bot DE\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(DE\bot \left( SAC \right)\Rightarrow \left( SDE \right)\bot \left( SAC \right)\).
Ta có \(\left. \begin{array}{l}\left( {SDE} \right) \supset SD\\\left( {SDE} \right) \bot \left( {SAC} \right)\end{array} \right\} \Rightarrow \left( \alpha \right) \equiv \left( {SDE} \right).\)
Vậy thiết diện là tam giác
Ta có \(SD=\sqrt{S{{A}^{2}}+D{{A}^{2}}}=a\sqrt{2};\text{ }SE=\sqrt{S{{A}^{2}}+A{{E}^{2}}}=a\sqrt{2}\); \(DE=AC=DC\sqrt{2}=a\sqrt{2}\).
Do đó tam giác \(SDE\) đều có cạnh \(a\sqrt{2}\) nên \({{S}_{\Delta \,SDE}}=\frac{S{{D}^{2}}\sqrt{3}}{4}=\frac{{{a}^{2}}\sqrt{3}}{2}\).
Chọn C









