Cho hình chóp đều S.ABC. Mặt phẳng ( alpha ) qua A song song với BC và vuông góc với mặt phẳng ( SB

Câu hỏi
Nhận biếtCho hình chóp đều \(S.ABC\). Mặt phẳng \(\left( \alpha \right)\) qua \(A\), song song với \(BC\) và vuông góc với mặt phẳng \(\left( SBC \right)\). Thiết diện tạo bởi \(\left( \alpha \right)\) với hình chóp đã cho là:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
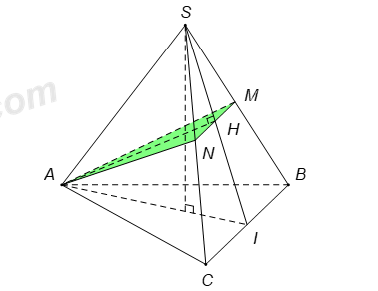
Gọi \(I\) là trung điểm \(BC\).
Trong tam giác \(SAI\) kẻ \(AH\bot SI\) \(\left( H\in SI \right)\).
Trong tam giác \(SBC\), qua \(H\) kẻ đường song song với \(BC\), cắt \(SC\) ở \(M\), cắt \(SB\) ở \(N\).
Qua cách dựng ta có \(BC\parallel \left( AMN \right).\)
Và \(\left\{ \begin{array}{l}SI \bot AH\\SI \bot MN{\rm{ }}\left( {{\rm{do }}SI \bot BC} \right)\end{array} \right. \Rightarrow SI \bot \left( {AMN} \right) \Rightarrow \left( {SBC} \right) \bot \left( {AMN} \right).\)
Từ và , suy ra thiết diện cần tìm là tam giác .
Dễ thấy \(H\) là trung điểm của \(MN\) mà \(AH\bot \left( SBC \right)\) suy ra \(AH\bot MN\). Tam giác \(AMN\) có đường cao \(AH\) vừa là trung tuyến nên nó là tam giác cân đỉnh \(A\).
Chọn B









