Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D đáy lớn AB; cạnh bên SA vuông góc vớ

Câu hỏi
Nhận biếtCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), đáy lớn \(AB\); cạnh bên \(SA\) vuông góc với đáy. Gọi \(Q\) là điểm trên cạnh \(SA\) và \(Q\ne A,\) \(Q\ne S\); \(M\) là điểm trên đoạn \(AD\) và \(M\ne A\). Mặt phẳng \(\left( \alpha \right)\) qua \(QM\) và vuông góc với mặt phẳng \(\left( SAD \right)\). Thiết diện tạo bởi \(\left( \alpha \right)\) với hình chóp đã cho là:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
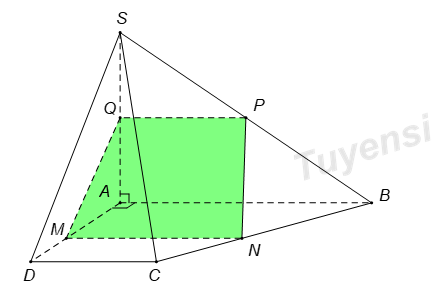
Ta có \(\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right)\). Mà \(\left( \alpha \right)\bot \left( SAD \right)\) suy ra \(AB\parallel \left( \alpha \right)\).
Qua \(M\) kẻ đường thẳng song song với \(AB\) cắt \(BC\) tại \(N\).
Qua \(E\) kẻ đường thẳng song song với \(AB\) cắt \(SB\) tại \(P\).
Khi đó thiết diện là hình thang \(MNPQ\) (do \(MN\parallel PQ\().
Vì \(AB\bot \left( SAD \right)\) suy ra \(MN\bot \left( SAD \right)\) nên \(MN\bot MQ\).
Do đó thiết diện \(MNPQ\) là hình thang vuông tại Q và \(M\).
Chọn C









