Cho hình lập phương ABCD.A’B’C’D’. Gọi alpha là góc giữa AC’ và mặt phẳng (A’BCD’). Chọn khẳng định

Câu hỏi
Nhận biếtCho hình lập phương ABCD.A’B’C’D’. Gọi \(\alpha \) là góc giữa AC’ và mặt phẳng (A’BCD’). Chọn khẳng định đúng trong các khẳng định sau?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
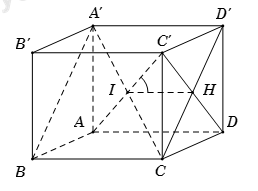
Gọi \(A'C \cap AC' = I;{\rm{ }}C'D \cap CD' = H\).
Ta có \(\left\{ \begin{array}{l}C'D \bot CD'\\C'D \bot A'D'\,\,\left( {A'D' \bot \left( {CDD'C'} \right)} \right)\end{array} \right. \Rightarrow C'D \bot \left( {A'BCD'} \right)\)
Hay \(C'H \bot \left( {A'BCD'} \right)\)
\( \Rightarrow HI\) là hình chiếu vuông góc của C’I trên (A’BCD’)
Do đó \(\widehat {\left( {AC',\left( {A'BCD'} \right)} \right)} = \widehat {\left( {C'I;\left( {A'BCD'} \right)} \right)} = \widehat {\left( {C'I;HI} \right)} = \widehat {C'IH}.\)
Trong tam giác vuông C’HI vuông tại H, có \(\tan \widehat {C'IH} = \frac{{C'H}}{{IH}} = \frac{{\frac{{AB\sqrt 2 }}{2}}}{{\frac{{AB}}{2}}} = \sqrt 2 .\)
Chọn D.









